如图所示，在△ABC中，∠ABC与∠ACB的平分线交于点O，根据下列条件，求出∠BOC的度数．
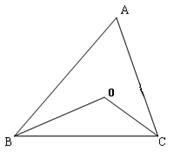
（1）已知∠ABC+∠ACB=100°，则∠BOC= ．
（2）已知∠A=90°，求∠BOC的度数．
（3）从上述计算中，你能发现∠BOC与∠A的关系吗？请直接写出∠B0C与∠A的关系．
与
的大小，并写出理由；
+
的度数．
方向走了
到达A点，再从A点沿着北偏西
代表
，画出示意图，并量出示意图中线段BO的长度．
，其中
．
．
．相关知识点
推荐套卷
如图所示，在△ABC中，∠ABC与∠ACB的平分线交于点O，根据下列条件，求出∠BOC的度数．
（1）已知∠ABC+∠ACB=100°，则∠BOC= ．
（2）已知∠A=90°，求∠BOC的度数．
（3）从上述计算中，你能发现∠BOC与∠A的关系吗？请直接写出∠B0C与∠A的关系．
粤公网安备 44130202000953号