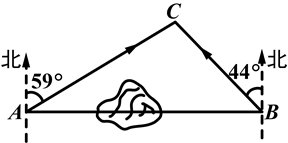
如图，我国甲、乙两艘海监执法船某天在某岛附近海域巡航，某一时刻这两艘船分别位于该岛正西方向的A处和正东方向的B处，这时两船同时接到立即赶往C处海域巡查的任务，并测得C处位于A处北偏东59°方向，位于B处北偏西44°方向．若甲、乙两船分别沿AC，BC方向航行，且平均速度分别是20海里／时，18海里／时，试估算哪艘船先赶到C处．
(参考数据：cos59°≈0.52，cos44°≈0.72)