如图1是小志同学书桌上的一个电子相框，将其侧面抽象为如图2所示的几何图形，已知BC=BD=15cm，∠CBD=40°，则点B到CD的距离为 cm（参考数据sin20°≈0.342，cos20°≈0.940，sin40°≈0.643，cos40°≈0.766，结果精确到0.1cm，可用科学计算器）．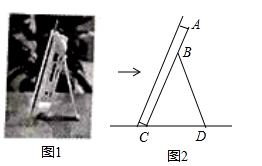
=．
个图形需根火柴棒。
相关知识点
推荐套卷
如图1是小志同学书桌上的一个电子相框，将其侧面抽象为如图2所示的几何图形，已知BC=BD=15cm，∠CBD=40°，则点B到CD的距离为 cm（参考数据sin20°≈0.342，cos20°≈0.940，sin40°≈0.643，cos40°≈0.766，结果精确到0.1cm，可用科学计算器）．
粤公网安备 44130202000953号