(本小题满分16分)如图,在平面直角坐标系 中,
中,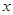 轴在地平面上,
轴在地平面上, 轴垂直于地面,
轴垂直于地面,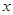 轴、
轴、 轴上的单位长度都为
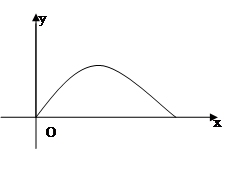
轴上的单位长度都为 ,某炮位于坐标原点处,炮弹发射后,其路径为抛物线
,某炮位于坐标原点处,炮弹发射后,其路径为抛物线 的一部分,其中
的一部分,其中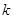 与炮弹的发射角有关且
与炮弹的发射角有关且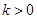 .
.
(1)当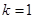 时,求炮弹的射程;
时,求炮弹的射程;
(2)对任意正数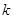 ,求炮弹能击中的飞行物的高度
,求炮弹能击中的飞行物的高度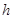 的取值范围;
的取值范围;
(3)设一飞行物(忽略大小)的高度为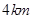 ,试求它的横坐标
,试求它的横坐标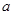 不超过多少
不超过多少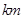 时,炮弹可以击中它.(答案精确到
时,炮弹可以击中它.(答案精确到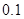 ,
, 取
取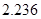 )
)
相关知识点
推荐套卷
(本小题满分16分)如图,在平面直角坐标系 中,
中,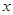 轴在地平面上,
轴在地平面上, 轴垂直于地面,
轴垂直于地面,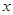 轴、
轴、 轴上的单位长度都为
轴上的单位长度都为 ,某炮位于坐标原点处,炮弹发射后,其路径为抛物线
,某炮位于坐标原点处,炮弹发射后,其路径为抛物线 的一部分,其中
的一部分,其中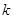 与炮弹的发射角有关且
与炮弹的发射角有关且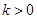 .
.
(1)当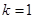 时,求炮弹的射程;
时,求炮弹的射程;
(2)对任意正数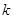 ,求炮弹能击中的飞行物的高度
,求炮弹能击中的飞行物的高度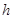 的取值范围;
的取值范围;
(3)设一飞行物(忽略大小)的高度为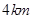 ,试求它的横坐标
,试求它的横坐标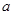 不超过多少
不超过多少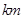 时,炮弹可以击中它.(答案精确到
时,炮弹可以击中它.(答案精确到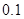 ,
, 取
取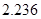 )
)