一位同学想利用树的影长测量树高，他在某一时刻测得长为1m的竹竿的影长为0.9m，但当他马上测量树的影长时，因树靠近一幢建筑物，影子不全落在地面上，有一部分影子落在墙上，如图，他先测得留在墙上的影子高CD为1.2m，又测得地面上的影子长BC为2.7m，则树高AB为多少？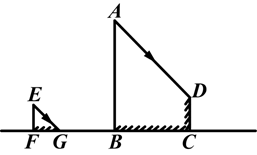
相关试题
一位同学想利用树的影长测量树高，他在某一时刻测得长为1m的竹竿的影长为0.9m，但当他马上测量树的影长时，因树靠近一幢建筑物，影子不全落在地面上，有一部分影子落在墙上，如图，他先测得留在墙上的影子高CD为1.2m，又测得地面上的影子长BC为2.7m，则树高AB为多少？
的最小值为．
,
,
,化简
=．
的解为．
、
两地，用大、小两种货车共20辆，恰好能一次性装完这批白砂糖．已知这两种货车的载重量分别为15吨/辆和10吨/辆，运往
辆，其余货车前往
，求w与a的关系式（用含有
粤公网安备 44130202000953号