已知函数
在同一半周期内的图象过点
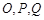，其中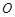
为坐标原点，
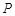为函数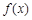
图象的最高点，
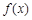为函数的图象与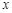
轴的正半轴的交点．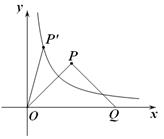 
（1）求证：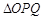
为等腰直角三角形．
（2）将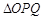绕原点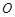按逆时针方向旋转角
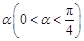，得到
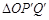，若点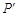
恰好落在曲线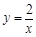
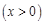上（如图所示），试判断点
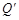是否也落在曲线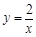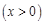上，并说明理由
相关试题
上的最小值为
，试将
对于定义域内任意一个
都有
，且
.（1）求
的值；（2）用定义证明
在
上是增函数
的最大值和最小值。
的图像过原点，且
，试求
P，求a取值？
A=A,求m的范围？推荐套卷
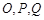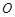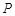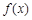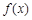已知函数在同一半周期内的图象过点，其中为坐标原点，为函数图象的最高点，为函数的图象与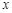轴的正半轴的交点．
（1）求证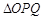：为等腰直角三角形．
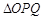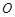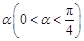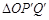（2）将绕原点按逆时针方向旋转角，得到，若点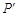恰好落在曲线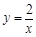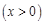上（如图所示），试判断点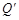是否也落在曲线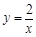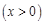上，并说明理由
粤公网安备 44130202000953号