(8 分)如图,反比例函数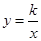 的图象经过点A(
的图象经过点A(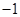 ,4),直线
,4),直线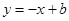 (
( )与双曲线
)与双曲线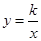 在第二、四象限分别相交于P,Q 两点,与x轴、y 轴分别相交于C,D 两点.
在第二、四象限分别相交于P,Q 两点,与x轴、y 轴分别相交于C,D 两点.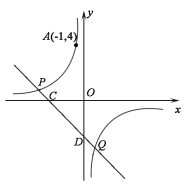
(1)求k 的值;
(2)当 时,求△OCD 的面积;
时,求△OCD 的面积;
(3)连接OQ,是否存在实数b,使得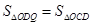 ? 若存在,请求出b 的值;若不存在,请说明理由.
? 若存在,请求出b 的值;若不存在,请说明理由.
相关知识点
推荐套卷
(8 分)如图,反比例函数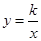 的图象经过点A(
的图象经过点A(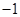 ,4),直线
,4),直线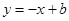 (
( )与双曲线
)与双曲线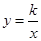 在第二、四象限分别相交于P,Q 两点,与x轴、y 轴分别相交于C,D 两点.
在第二、四象限分别相交于P,Q 两点,与x轴、y 轴分别相交于C,D 两点.
(1)求k 的值;
(2)当 时,求△OCD 的面积;
时,求△OCD 的面积;
(3)连接OQ,是否存在实数b,使得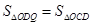 ? 若存在,请求出b 的值;若不存在,请说明理由.
? 若存在,请求出b 的值;若不存在,请说明理由.