如图,△ABC中,AB=AC,点P是三角形右外一点,且∠APB=∠ABC.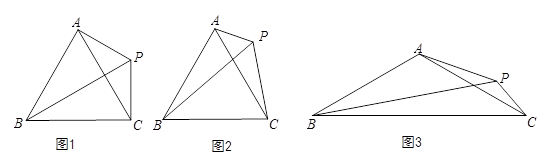
(1)如图1,若∠BAC=60°,点P恰巧在∠ABC的平分线上,PA=2,求PB的长;
(2)如图2,若∠BAC=60°,探究PA,PB,PC的数量关系,并证明;
(3)如图3,若∠BAC=120°,请直接写出PA,PB,PC的数量关系.
相关知识点
推荐套卷
如图,△ABC中,AB=AC,点P是三角形右外一点,且∠APB=∠ABC.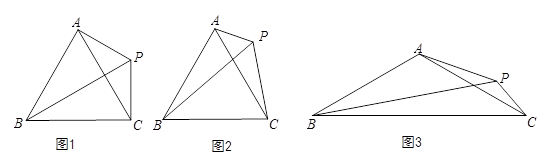
(1)如图1,若∠BAC=60°,点P恰巧在∠ABC的平分线上,PA=2,求PB的长;
(2)如图2,若∠BAC=60°,探究PA,PB,PC的数量关系,并证明;
(3)如图3,若∠BAC=120°,请直接写出PA,PB,PC的数量关系.