（本题8分）某学校举行“社会主义核心价值观”知识比赛活动，全体学生都参加比赛，学校对参赛学生均给与表彰，并设置一、二、三等奖和纪念奖共四个奖项，赛后将获奖情况绘制成如下所示的两幅不完整的统计图，请根据图中所给的信息，解答下列问题：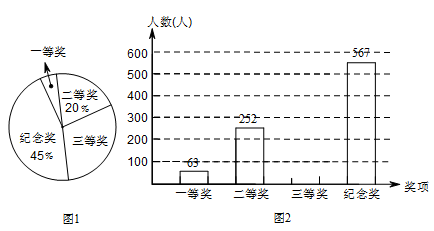
（1）该校共有 名学生；
（2）在图1中，“三等奖”随对应扇形的圆心角度数是 ；
（3）将图2补充完整；
（4）从该校参加本次比赛活动的学生中随机抽查一名．求抽到获得一等奖的学生的概率．
相关试题
，其中
．如图所示，
A、B两城市相距100 km，现计划在这两座城市间修建一条高速公路（即线段AB），经
测量，森林保护中心P在A城市的北偏东
和B城市的北偏西
的方向上，已知森林保护区的范围在以P点为圆心，50 km为半径的圆形区域内，请问计划修建的这条高速公路会不会穿越保护区，为什么？（参考数据：
）
如图，已知∠ACB＝90°，AC＝BC，BE⊥CE于E，AD⊥CE于D，CE与AB相交于F．
粤公网安备 44130202000953号