如图①，P为△ABC内一点，连接PA、PB、PC，在△PAB、△PBC和△PAC中，如果存在一个三角形与△ABC相似，那么就称P为△ABC的自相似点．
（1）如图②，已知Rt△ABC中，∠ACB=90°，∠ACB＞∠A，CD是AB上的中线，过点B作BE⊥CD，垂足为E，试说明E是△ABC的自相似点．
（2）如图③，在△ABC中，∠A＜∠B＜∠C．
①利用尺规作出△ABC的自相似点P（不写出作法，保留作图痕迹）；
②如果△ABC的内心P是该三角形的自相似点，请直接写出该三角形三个内角的度数．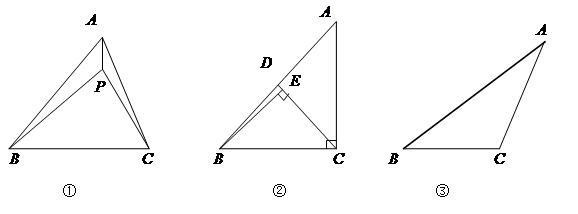
相关试题
战胜乙队的概率．甲、乙两篮球运动员上赛季每场比赛的得分如下：
甲15，24，25，31，31，36，36，37，39，44，50．
乙8，13，14，16，23，26，28，33，38，39，51．
小莉用如图的方式来表示甲、乙的得分．
（1）请在右侧补全乙的得分；
（2）用不等号填空：
;
;
（3）请说出此种表示方式的优点．
、
的方程组
，的解是
，求
的值．
．相关知识点
推荐套卷
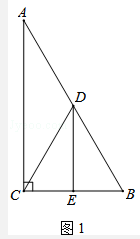
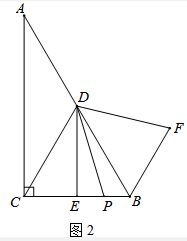
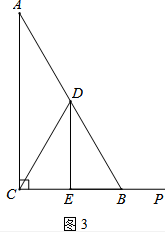
粤公网安备 44130202000953号