某厂生产产品x件的总成本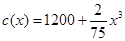
（万元）,已知产品单价P（万元）与产品件数x满足:
,生产100件这样的产品单价为50万元．
（1）设产量为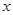
件时,总利润为
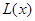（万元）,求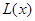的解析式;
（2）产量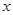定为多少件时总利润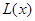（万元）最大?并求最大值（精确到1万元）．
相关试题
所对的边分别为a,b,c,
，求a．
满足
,
，
，求证：数列
是等比数列，并求其公比；
时令
，记数列
的前
项和为
，数列
，求证：对任
为定值．
，
时，求
的最大值；
时，若对任意
，都有
恒成立，且
的最大值为2，求
的表达式．
，离心率
，且过点
，
以
为直角顶点，边
与椭圆交于
两点，求
面积的最大值．
平面
,
为等边三角形，
平面
，求CD长度；推荐套卷
某厂生产产品x件的总成本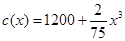（万元）,已知产品单价P（万元）与产品件数x满足:,生产100件这样的产品单价为50万元．
（1）设产量为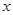件时,总利润为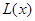（万元）,求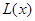的解析式;
（2）产量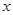定为多少件时总利润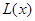（万元）最大?并求最大值（精确到1万元）．
粤公网安备 44130202000953号