如图四棱柱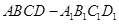 中,
中,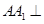 面
面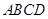 ,四边形
,四边形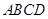 为梯形,
为梯形,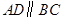 ,且
,且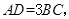 过
过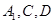 三点的平面记为
三点的平面记为 ,
,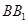 与
与 的交点为
的交点为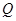 ,则以下四个结论:
,则以下四个结论:
①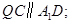 ②
②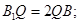 ③直线
③直线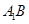 与直线
与直线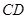 相交;④四棱柱被平面
相交;④四棱柱被平面 分成的上下两部分的体积相
分成的上下两部分的体积相
等,其中正确的个数为( )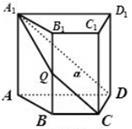
| A.1个 | B.2个 | C.3个 | D.4个 |
推荐套卷
如图四棱柱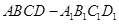 中,
中,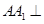 面
面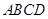 ,四边形
,四边形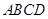 为梯形,
为梯形,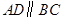 ,且
,且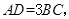 过
过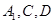 三点的平面记为
三点的平面记为 ,
,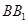 与
与 的交点为
的交点为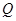 ,则以下四个结论:
,则以下四个结论:
①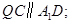 ②
②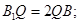 ③直线
③直线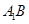 与直线
与直线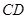 相交;④四棱柱被平面
相交;④四棱柱被平面 分成的上下两部分的体积相
分成的上下两部分的体积相
等,其中正确的个数为( )
| A.1个 | B.2个 | C.3个 | D.4个 |