如图（1），在正方形ABCD中，P是对角线AC上的一点，点E在BC的延长线上，且PE＝PB．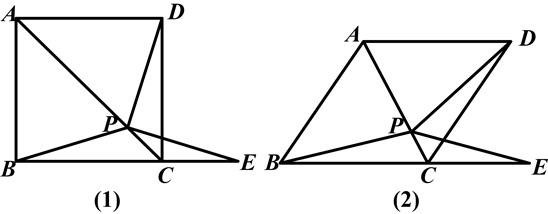
（1）求证：△BCP≌△DCP；
（2）求证：∠DPE＝∠ABC；
（3）把正方形ABCD改为菱形，其他条件不变，如图（2），如果∠ABC＝58°，那么∠DPE＝________度．
如图（1），在正方形ABCD中，P是对角线AC上的一点，点E在BC的延长线上，且PE＝PB．
（1）求证：△BCP≌△DCP；
（2）求证：∠DPE＝∠ABC；
（3）把正方形ABCD改为菱形，其他条件不变，如图（2），如果∠ABC＝58°，那么∠DPE＝________度．
=0，求方程
+bx=1的解.
粤公网安备 44130202000953号