如图,若观测点的高度为h,观测者视线能达到的最远距离为d,则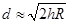 ,其中R是地球半径(通常取6400km).
,其中R是地球半径(通常取6400km).
(1)小丽站在海边一块岩石上,眼睛离地面的高度为20m,此时小丽视线能达到的最远距离为多少千米?
(2)已知泰山到海边的最近距离是216000m,泰山的海拔高度为1545m,利用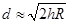 计算,判断站在泰山之巅能否看到大海.
计算,判断站在泰山之巅能否看到大海.
如图,若观测点的高度为h,观测者视线能达到的最远距离为d,则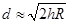 ,其中R是地球半径(通常取6400km).
,其中R是地球半径(通常取6400km).
(1)小丽站在海边一块岩石上,眼睛离地面的高度为20m,此时小丽视线能达到的最远距离为多少千米?
(2)已知泰山到海边的最近距离是216000m,泰山的海拔高度为1545m,利用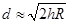 计算,判断站在泰山之巅能否看到大海.
计算,判断站在泰山之巅能否看到大海.