个体经营户小李在蔬菜批发市场上了解到如下信息:
| 蔬菜品种 |
西红柿 |
红辣椒 |
黄瓜 |
茄子 |
| 批发价(元/千克) |
1.6 |
4 |
1.2 |
1.1 |
| 零售价(元/千克) |
2.0 |
5 |
1.4 |
1.3 |
他从批发市场上批发了44千克的西红柿和红辣椒,共用了116元,到小菜市场当天就卖完了.问:小李当天能赚多少钱?
相关知识点
推荐套卷



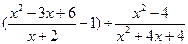 ,其中
,其中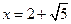 .
.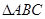 ,使底边长为a,底边上的高为
,使底边长为a,底边上的高为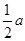 .(要求:写出已知求作,保留作图痕迹,在所作图中标出必要的字母,不写作法和结论)
.(要求:写出已知求作,保留作图痕迹,在所作图中标出必要的字母,不写作法和结论)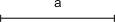
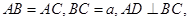 且
且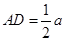
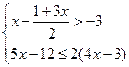
 粤公网安备 44130202000953号
粤公网安备 44130202000953号