(本题满分13分)
已知函数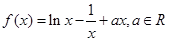
.
（I）若函数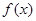
在
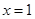处的切线与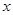
轴平行，求
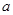值；
（II）讨论函数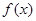在其定义域内的单调性；
（III）定义：若函数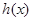
在区间D上任意
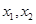都有
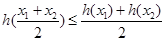，则称函数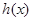是区间D上的凹函数.设函数
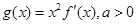，其中
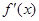是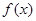的导函数．根据上述定义，判断函数
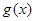是否为其定义域内的凹函数，并说明理由.
设
的定义域；
元，若销售价为
元，可卖出
元，销售量就减少
求
的值。
，
，若
，
的值。推荐套卷
(本题满分13分)
已知函数.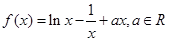
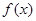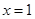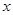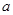（I）若函数在处的切线与轴平行，求值；
（II）讨论函数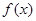在其定义域内的单调性；
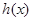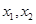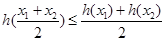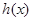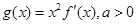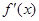（III）定义：若函数在区间D上任意都有，则称函数是区间D上的凹函数.设函数，其中是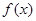的导函数．根据上述定义，判断函数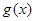是否为其定义域内的凹函数，并说明理由.
粤公网安备 44130202000953号