某同学用"五点法"画函数
在某一个周期内的图象时,列表并填入了部分数据,如下表:
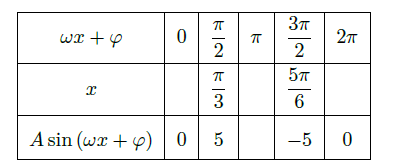
(Ⅰ)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数
的解析式;
(Ⅱ)将
图象上所有点向左平行移动
个单位长度,得到
图象,求
的图象离原点
最近的对称中心.
相关知识点
推荐套卷
某同学用"五点法"画函数
在某一个周期内的图象时,列表并填入了部分数据,如下表:

(Ⅰ)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数
的解析式;
(Ⅱ)将
图象上所有点向左平行移动
个单位长度,得到
图象,求
的图象离原点
最近的对称中心.