（本小题共12分）已知E是矩形ABCD（如图1）边CD上的一点，现沿AE将△DAE折起至△D1AE（如图2），并且平面D1AE⊥平面ABCE，图3为四棱锥D1—ABCE的主视图与左视图．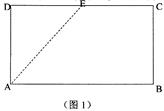
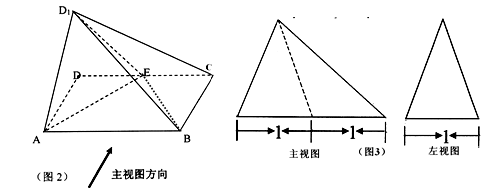
（1）求证：直线BE⊥平面D1AE；
（2）求点A到平面D1BC的距离．
相关试题
，在同一周期内，
时，
取得最大值
；当
时，
.
时，函数
有两个零点，求实数
的取值范围．
,
).
|=|
|，求角α的值；
，求
的值.
与
平行，求实数
的值.
.
；（Ⅱ）已知
，求
,求
;
的夹角为
，求
.相关知识点
推荐套卷
（本小题共12分）已知E是矩形ABCD（如图1）边CD上的一点，现沿AE将△DAE折起至△D1AE（如图2），并且平面D1AE⊥平面ABCE，图3为四棱锥D1—ABCE的主视图与左视图．
（1）求证：直线BE⊥平面D1AE；
（2）求点A到平面D1BC的距离．
粤公网安备 44130202000953号