(本小题满分12分)某高中数学竞赛培训在某学段共开设有初等代数、平面几何、初等数论和微积分初步共四门课程,要求初等数论、平面几何都要合格,且初等代数和微积分初步至少有一门合格,则能取得参加数学竞赛复赛的资格.现有甲、乙、丙三位同学报名参加数学竞赛培训,每一位同学对这四门课程考试是否合格相互独立,其合格的概率均相同(见下表),且每一门课程是否合格相互独立.
(Ⅰ)求甲同学取得参加数学竞赛复赛的资格的概率;
(Ⅱ)记 表示三位同学中取得参加数学竞赛复赛的资格的人数,求
表示三位同学中取得参加数学竞赛复赛的资格的人数,求 的分布列及期望
的分布列及期望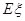 .
.
相关知识点
推荐套卷
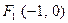 出发,经直线
出发,经直线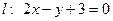 上一点
上一点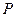 反射后,恰好穿过点
反射后,恰好穿过点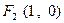 .(Ⅰ)求点
.(Ⅰ)求点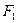 关于直线
关于直线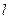 的对称点
的对称点 的坐标;
的坐标;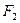 为焦点且过点
为焦点且过点 的方程;
的方程;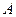 、
、 两点,点
两点,点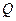 为线段
为线段 上的动点,求点
上的动点,求点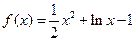 .
. 在区间
在区间 (
( 为自然对数的底)上的最大值和最小值;
为自然对数的底)上的最大值和最小值; 上,函数
上,函数 的图象的下方;
的图象的下方; ≥
≥
 .
.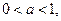 下列不等式一定成立的是()
下列不等式一定成立的是() ;
;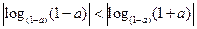 ;
; ;
;
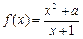 (其中
(其中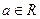 ).
). 在点
在点 处的切线为
处的切线为 ,求实数
,求实数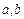 的值;
的值; 直线AB过抛物线x2=2py(p>0)的焦点F,并与其相交于A、B两点,Q是线段AB的中点,M是抛物线的准线与y轴的交点,O是坐标原点.
直线AB过抛物线x2=2py(p>0)的焦点F,并与其相交于A、B两点,Q是线段AB的中点,M是抛物线的准线与y轴的交点,O是坐标原点.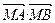 的取值范围;
的取值范围; ;
;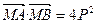 ,△ABN的面积的取值范围为[5
,△ABN的面积的取值范围为[5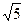 ,20
,20 粤公网安备 44130202000953号
粤公网安备 44130202000953号