在求1+6+62+63+64+65+66+67+68+69的值时，小林发现：从第二个加数起每一个加数都是前一个加数的6倍，于是她设：
S=1+6+62+63+64+65+66+67+68+69①
然后在①式的两边都乘以6，得：
6S=6+62+63+64+65+66+67+68+69+610②
②﹣①得6S﹣S=610﹣1，即5S=610﹣1，所以S=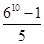
，得出答案后，爱动脑筋的小林想：如果把“6”换成字母“a”（a≠0且a≠1），能否求出1+a+a2+a3+a4+…+a2014的值？你的答案是______________________．
相关试题
如图，一条街道旁有A，B，C，D，E五间店面，某矿泉水经销商统计各店面每周所需矿泉水的数量均相等．他计划在这五间店面中设立矿泉水供应点．若仅考虑这五间店面的用户取水所走路程之和最小，可以选择的地点应在________间店面．
相关知识点
推荐套卷
粤公网安备 44130202000953号