某商场计划购进冰箱、彩电进行销售,相关信息如下表: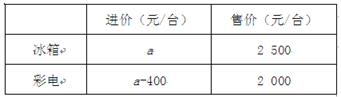
(1)若商场用80 000元购进冰箱的数量与用64 000元购进彩电的数量相等,求表中a的值.
(2)在(1)的条件下,为了满足市场需求,商场决定用不超过9万元采购冰箱、彩电共50台,且冰箱的数量不少于彩电数量的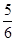 .
.
①该商场有哪几种进货方式?
②若该商场将购进的冰箱、彩电全部售出,获得的最大利润为w元,请用所学的函数知识求出w的值.
相关知识点
推荐套卷
某商场计划购进冰箱、彩电进行销售,相关信息如下表:
(1)若商场用80 000元购进冰箱的数量与用64 000元购进彩电的数量相等,求表中a的值.
(2)在(1)的条件下,为了满足市场需求,商场决定用不超过9万元采购冰箱、彩电共50台,且冰箱的数量不少于彩电数量的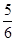 .
.
①该商场有哪几种进货方式?
②若该商场将购进的冰箱、彩电全部售出,获得的最大利润为w元,请用所学的函数知识求出w的值.