如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.
(1)求A点坐标及线段AB的长;
(2)若点P由点A出发以每秒1个单位的速度沿AB边向点B移动,1秒后点Q也由点A出发以每秒7个单位的速度沿A-O-C-B的方向向点B移动,当其中一个点到达终点时另一个点也停止移动,点P的移动时间为t秒.
①当PQ⊥AC时,求t的值;
②当PQ∥AC时,对于抛物线对称轴上一点H,当点H的纵坐标满足条件_________时,∠HOQ<∠POQ.(直接写出答案)
相关知识点
推荐套卷
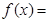
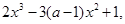 其中
其中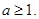
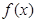 的单调区间;
的单调区间;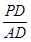 =
=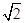 ,求平面PBE与平面ABCD所成的锐二面角的大小.
,求平面PBE与平面ABCD所成的锐二面角的大小.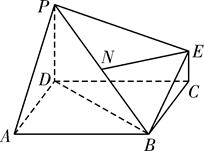
 c-2b,
c-2b, ,BC边上的中线AM的长为
,BC边上的中线AM的长为 ,求△ABC的面积.
,求△ABC的面积.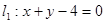 与直线
与直线 相交于点P,
相交于点P,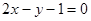 平行的直线方程;
平行的直线方程; 粤公网安备 44130202000953号
粤公网安备 44130202000953号