(本小题满分13分)某学校实验室有浓度为 和
和 的两种
的两种 溶液.在使用之前需要重新配制溶液,具体操作方法为取浓度为
溶液.在使用之前需要重新配制溶液,具体操作方法为取浓度为 和
和 的两种
的两种 溶液各
溶液各 分别装入两个容积都为
分别装入两个容积都为 的锥形瓶
的锥形瓶 中,先从瓶
中,先从瓶 中取出
中取出 溶液放入
溶液放入 瓶中,充分混合后,再从
瓶中,充分混合后,再从 瓶中取出
瓶中取出 溶液放入
溶液放入 瓶中,再充分混合.以上两次混合过程完成后算完成一次操作.设在完成第
瓶中,再充分混合.以上两次混合过程完成后算完成一次操作.设在完成第 次操作后,
次操作后, 瓶中溶液浓度为
瓶中溶液浓度为 ,
, 瓶中溶液浓度为
瓶中溶液浓度为 .
.
(1)请计算 ,并判定数列
,并判定数列 是否为等比数列?若是,求出其通项公式;若不是,请说明理由;
是否为等比数列?若是,求出其通项公式;若不是,请说明理由;
(2)若要使得 两个瓶中的溶液浓度之差小于
两个瓶中的溶液浓度之差小于 ,则至少要经过几次?
,则至少要经过几次?
相关知识点
推荐套卷
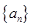 中,已知
中,已知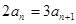 且
且
 是这个等比数列中的项吗?如果是,指明是第几项;如果不是,请说明理由.
是这个等比数列中的项吗?如果是,指明是第几项;如果不是,请说明理由.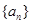 中,
中,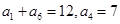 ,记其前n项和为
,记其前n项和为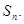
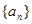 的通项公式
的通项公式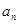 ;
;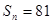 ,求n
,求n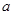 ,
,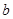 ,
,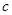 成等比数列,其公比为3,如果
成等比数列,其公比为3,如果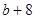 ,
,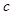 成等差数列,求这三个数.
成等差数列,求这三个数.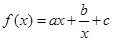 (
(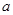 >0)的图象在点
>0)的图象在点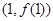 处的切线方程为
处的切线方程为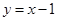 .
. ;
;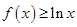 在
在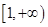 上恒成立,求
上恒成立,求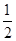 +
+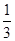 +…+
+…+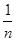 >
> +
+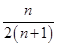
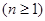 .
.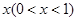 , 则出厂价相应提高的比例为
, 则出厂价相应提高的比例为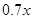 ,年销售量也适当增加.设年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量
,年销售量也适当增加.设年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量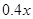 ,为使本年度的年利润比上年度有所增加,则投入成本增加的比例
,为使本年度的年利润比上年度有所增加,则投入成本增加的比例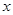 应在什么范围内?
应在什么范围内?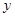 (辆)关于
(辆)关于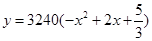 ,则当
,则当 粤公网安备 44130202000953号
粤公网安备 44130202000953号