（本小题满分8分）区教育局为了丰富初中学生的大课间活动，要求各学校开展形式多样的阳光体育活动-教育局就“学生体育活动兴趣爱好”的问题，随机调查了本区的部分初中生。并根据调查结果绘制成以下图表：
某初中学生大课间活动情况统计图 某初中学生大课间活动情况扇形统计图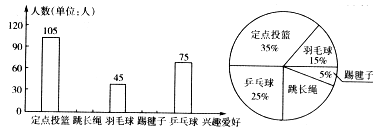
（1）请将条形图空缺部分补充完整；
（2）请计算出教育局共随机调查了本区多少名初中生?并计算出这些学生中参加跳长绳人数所在扇形的圆心角的度数；
（3）若全区共有12000名初中生，请你估算出参加踢毽子的学生人数．
（操作发现）
如图①，在边长为1个单位长度的小正方形组成的网格中， 的三个顶点均在格点上．
（1）请按要求画图：将 绕点 按顺时针方向旋转 ，点 的对应点为 ，点 的对应点为 ，连接 ；
（2）在（1）所画图形中， ．
（问题解决）
如图②，在等边三角形 中， ，点 在 内，且 ， ，求 的面积．
小明同学通过观察、分析、思考，对上述问题形成了如下想法：
想法一：将 绕点 按顺时针方向旋转 ，得到△ ，连接 ，寻找 ， ， 三条线段之间的数量关系；
想法二：将 绕点 按逆时针方向旋转 ，得到△ ，连接 ，寻找 ， ， 三条线段之间的数量关系．
请参考小明同学的想法，完成该问题的解答过程．（一种方法即可）
（灵活运用）
如图③，在四边形 中， ，垂足为 ， ， ， ， 为常数），求 的长（用含 的式子表示）．
某公司组织员工到附近的景点旅游，根据旅行社提供的收费方案，绘制了如图所示的图象，图中折线 表示人均收费 （元）与参加旅游的人数 （人）之间的函数关系．
（1）当参加旅游的人数不超过10人时，人均收费为 元；
（2）如果该公司支付给旅行社3600元，那么参加这次旅游的人数是多少？
， 两地被大山阻隔，若要从 地到 地，只能沿着如图所示的公路先从 地到 地，再由 地到 地．现计划开凿隧道 ， 两地直线贯通，经测量得： ， ， ，求隧道开通后与隧道开通前相比，从 地到 地的路程将缩短多少？（结果精确到 ，参考数据： ，
粤公网安备 44130202000953号