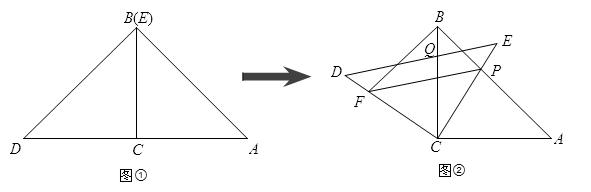
将两块全等的三角板如图①摆放，其中∠ACB=∠DCE=90°，∠A=∠D=45°，将图①中的△DCE顺时针旋转得图②，点P是AB与CE的交点，点Q是DE与BC的交点，在DC上取一点F，连接BE、FP，设BC=1，当BF⊥AB时，求△PBF面积的最大值。