（年广东广州14分）如图，梯形ABCD中，AB∥CD，∠ABC=90°，AB=3，BC=4，CD=5．点E为线段CD上一动点（不与点C重合），△BCE关于BE的轴对称图形为△BFE，连接CF．设CE=x，△BCF的面积为S1，△CEF的面积为S2．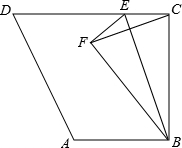
（1）当点F落在梯形ABCD的中位线上时，求x的值；
（2）试用x表示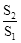
，并写出x的取值范围；
（3）当△BFE的外接圆与AD相切时，求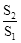的值．
相关试题
（年广东广州14分）如图，梯形ABCD中，AB∥CD，∠ABC=90°，AB=3，BC=4，CD=5．点E为线段CD上一动点（不与点C重合），△BCE关于BE的轴对称图形为△BFE，连接CF．设CE=x，△BCF的面积为S1，△CEF的面积为S2．
（1）当点F落在梯形ABCD的中位线上时，求x的值；
（2）试用x表示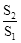，并写出x的取值范围；
（3）当△BFE的外接圆与AD相切时，求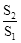的值．
粤公网安备 44130202000953号