(年山东日照14分)如图1,在菱形OABC中,已知OA=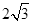 ,∠AOC=60°,抛物线y=ax2+bx+c(a≠0)经过O,C,B三点.
,∠AOC=60°,抛物线y=ax2+bx+c(a≠0)经过O,C,B三点.
(1)求出点B、C的坐标并求抛物线的解析式.
(2)如图2,点E是AC的中点,点F是AB的中点,直线AG垂直BC于点G,点P在直线AG上.
①当OP+PC的最小值时,求出点P的坐标;
②在①的条件下,连接PE、PF、EF得△PEF,问在抛物线上是否存在点M,使得以M,B,C为顶点的三角形与△PEF相似?若存在,请求出点M的坐标;若不存在,请说明理由.
(年山东日照14分)如图1,在菱形OABC中,已知OA=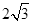 ,∠AOC=60°,抛物线y=ax2+bx+c(a≠0)经过O,C,B三点.
,∠AOC=60°,抛物线y=ax2+bx+c(a≠0)经过O,C,B三点.
(1)求出点B、C的坐标并求抛物线的解析式.
(2)如图2,点E是AC的中点,点F是AB的中点,直线AG垂直BC于点G,点P在直线AG上.
①当OP+PC的最小值时,求出点P的坐标;
②在①的条件下,连接PE、PF、EF得△PEF,问在抛物线上是否存在点M,使得以M,B,C为顶点的三角形与△PEF相似?若存在,请求出点M的坐标;若不存在,请说明理由.