（年江苏宿迁附加10分）如图，已知抛物线y=ax2+bx+c（a＞0，c＜0）交x轴于点A，B，交y轴于点C，设过点A，B，C三点的圆与y轴的另一个交点为D．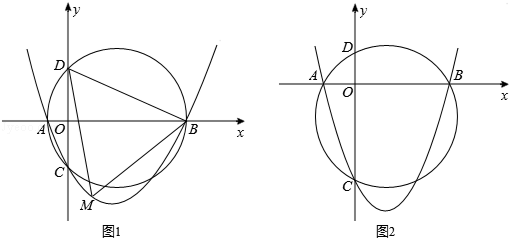
（1）如图1，已知点A，B，C的坐标分别为（﹣2，0），（8，0），（0，﹣4）；
①求此抛物线的表达式与点D的坐标；
②若点M为抛物线上的一动点，且位于第四象限，求△BDM面积的最大值；
（2）如图2，若a=1，求证：无论b，c取何值，点D均为定点，求出该定点坐标．
相关试题
（1）问题发现:如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE．
填空：①∠AEB的度数为 ___ ______；
②线段AD，BE之间的数量关系为 ___ ______．
（2）拓展探究
如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A，D ，E在同一直线上，CM为△DCE中 DE边上的高，连接BE，请判断∠AEB的度数及线段CM，AE，BE之间的数量关系，并说明理由．
，其中x=3,y=1
粤公网安备 44130202000953号