（年江苏常州9分）在平面直角坐标系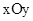
中，二次函数
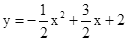的图像与
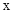轴交于点A，B（点B在点A的左侧），与
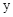轴交于点C，过动点H（0, 
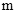）作平行于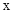轴的直线，直线与二次函数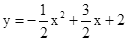的图像相交于点D，E.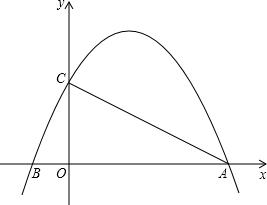
（1）写出点A,点B的坐标；
（2）若
，以DE为直径作⊙Q，当⊙Q与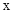轴相切时，求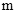的值；
（3）直线上是否存在一点F，使得△ACF是等腰直角三角形？若存在，求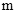的值；若不存在，请说明理由.
相关试题
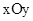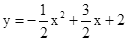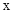（年江苏常州9分）在平面直角坐标系中，二次函数的图像与轴交于点A，B（点B在点A的左侧），与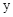轴交于点C，过动点H（0, 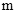）作平行于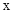轴的直线，直线与二次函数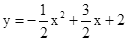的图像相交于点D，E.
（1）写出点A,点B的坐标；
（2）若，以DE为直径作⊙Q，当⊙Q与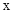轴相切时，求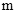的值；
（3）直线上是否存在一点F，使得△ACF是等腰直角三角形？若存在，求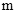的值；若不存在，请说明理由.
多800元，一、二、三年级捐款数是四、五、六年级捐款数的
全校共捐款多少元？
粤公网安备 44130202000953号