（年湖南娄底10分）如图甲，在△ABC中，∠ACB=90°，AC=4cm，BC=3cm．如果点P由点B出发沿BA方向向点A匀速运动，同时点Q由点A出发沿AC方向向点C匀速运动，它们的速度均为1cm/s．连接PQ，设运动时间为t（s）（0＜t＜4），解答下列问题：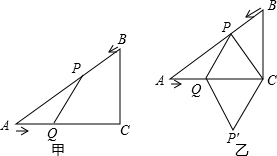
（1）设△APQ的面积为S，当t为何值时，S取得最大值？S的最大值是多少？
（2）如图乙，连接PC，将△PQC沿QC翻折，得到四边形PQP′C，当四边形PQP′C为菱形时，求t的值；′
（3）当t为何值时，△APQ是等腰三角形？
相关试题
已知：如图，在平面直角坐标系中，一次函数
的图象与反比例函数
的图象交于一、三象限内的A．B两点，与x轴交于C点，点A的坐标为（2,m)，点B的坐标为（n，－2），tan∠BOC＝
。
（l）求该反比例函数和一次函数的解析式；
（2）在x轴上有一点E（O点除外），使得△BCE与△BCO的面积相等，求出点E的坐标．
，其中
是不等式组
的整数解．
．
粤公网安备 44130202000953号