如图1,矩形ABCD中,点P从A出发,以3cm/s的速度沿边A→B→C→D匀速运动;同时点Q从B出发,沿边B→C→D匀速运动,当其中一个点到达终点时两点同时停止运动,设点P运动的时间为t s.△APQ的面积s(cm2)与t(s)之间函数关系的部分图像由图2中的曲线段OE与线段EF给出.
(1)点Q运动的速度为 cm/s,a﹦ cm2;
(2)若BC﹦3cm,
①写出当t>3时S关于t的函数关系式;
②在图(2)中画出①中相应的函数图像.
相关知识点
推荐套卷

 .
.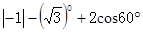
 )2+|-3|;
)2+|-3|;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号