给出下列四个命题:
①若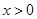 ,且
,且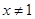 则
则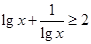 ;
;
②设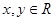 ,命题“若
,命题“若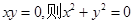 ”的否命题是真命题;
”的否命题是真命题;
③函数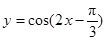 的一条对称轴是直线
的一条对称轴是直线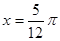 ;
;
④若定义在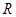 上的函数
上的函数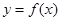 是奇函数,则对定义域内的任意
是奇函数,则对定义域内的任意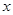 必有
必有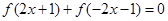 .
.
其中,所有正确命题的序号是 .
推荐套卷
给出下列四个命题:
①若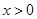 ,且
,且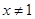 则
则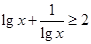 ;
;
②设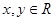 ,命题“若
,命题“若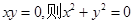 ”的否命题是真命题;
”的否命题是真命题;
③函数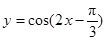 的一条对称轴是直线
的一条对称轴是直线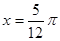 ;
;
④若定义在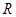 上的函数
上的函数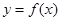 是奇函数,则对定义域内的任意
是奇函数,则对定义域内的任意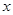 必有
必有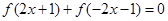 .
.
其中,所有正确命题的序号是 .