【原创】(本小题满分12分)为调查某市高中男生百米成绩,从该市高中男生中随机抽取20名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组 ,第二组
,第二组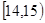 第五组
第五组 ,如图是按上述分组方法得到的频率分布直方图.根据有关规定,成绩小于16秒为达标.
,如图是按上述分组方法得到的频率分布直方图.根据有关规定,成绩小于16秒为达标.

(Ⅰ)求这组数据的众数、中位数及达标率(精确到0.01);
(Ⅱ)从这20人中不达标的人员中任取3人,至少二人成绩在16~17之间的概率.
推荐套卷
【原创】(本小题满分12分)为调查某市高中男生百米成绩,从该市高中男生中随机抽取20名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组 ,第二组
,第二组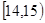 第五组
第五组 ,如图是按上述分组方法得到的频率分布直方图.根据有关规定,成绩小于16秒为达标.
,如图是按上述分组方法得到的频率分布直方图.根据有关规定,成绩小于16秒为达标.

(Ⅰ)求这组数据的众数、中位数及达标率(精确到0.01);
(Ⅱ)从这20人中不达标的人员中任取3人,至少二人成绩在16~17之间的概率.