设函数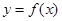 的定义域为
的定义域为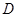 ,如果存在非零常数
,如果存在非零常数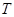 ,对于任意
,对于任意 ,都有
,都有 ,则称函数
,则称函数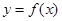 是“似周期函数”,非零常数
是“似周期函数”,非零常数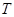 为函数
为函数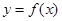 的“似周期”.现有下面四个关于“似周期函数”的命题:
的“似周期”.现有下面四个关于“似周期函数”的命题:
①如果“似周期函数”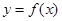 的“似周期”为-1,那么它是周期为2的周期函数;
的“似周期”为-1,那么它是周期为2的周期函数;
②函数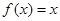 是“似周期函数”;
是“似周期函数”;
③函数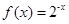 是“似周期函数”;
是“似周期函数”;
④如果函数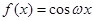 是“似周期函数”,那么“
是“似周期函数”,那么“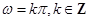 ”.
”.
其中是真命题的序号是 .(写出所有满足条件的命题序号)
相关知识点
推荐套卷
设函数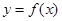 的定义域为
的定义域为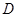 ,如果存在非零常数
,如果存在非零常数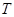 ,对于任意
,对于任意 ,都有
,都有 ,则称函数
,则称函数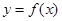 是“似周期函数”,非零常数
是“似周期函数”,非零常数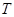 为函数
为函数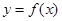 的“似周期”.现有下面四个关于“似周期函数”的命题:
的“似周期”.现有下面四个关于“似周期函数”的命题:
①如果“似周期函数”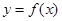 的“似周期”为-1,那么它是周期为2的周期函数;
的“似周期”为-1,那么它是周期为2的周期函数;
②函数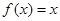 是“似周期函数”;
是“似周期函数”;
③函数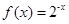 是“似周期函数”;
是“似周期函数”;
④如果函数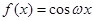 是“似周期函数”,那么“
是“似周期函数”,那么“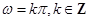 ”.
”.
其中是真命题的序号是 .(写出所有满足条件的命题序号)