某校学生会向全校1900名学生发起了爱心捐款活动，为了解捐款情况，学生会随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图①和图②，请根据相关信息，解答下列问题：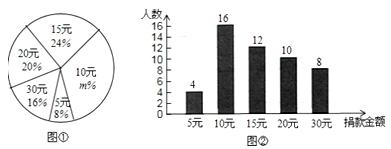
（1）本次接受随机抽样调查的学生人数为 ，图①中m的值是 ；
（2）求本次调查获取的样本数据的平均数、众数和中位数；
（3）根据样本数据，估计该校本次活动捐款金额为10元的学生人数．
相关试题
阅读下列材料：
问题：如图1，在正方形ABCD内有一点P，PA=
，PB=
，PC=1，求∠BPC的度数．
小明同学的想法是：已知条件比较分散，可以通过旋转变换将分散的已知条件集中在一起，于是他将△BPC绕点B逆时针旋转90°，得到了△BP′A（如图2），然后连结PP′．
请你参考小明同学的思路，解决下列问题：
(1) 图2中∠BPC的度数为 ；
(2) 如图3，若在正六边形ABCDEF内有一点P，且PA=
，PB=4，PC=2，则∠BPC的度数为 ，正六边形ABCDEF的边长为 ．
图1 图2 图3
如图，AC为⊙O的直径，AC=4，B、D分别在AC两侧的圆上，∠BAD=60°，BD与AC的交点为E．
(1) 求点O到BD的距离及∠OBD的度数；
(2) 若DE=2BE，求
的值和CD的长．
，BC=2，
，
．为了让更多的失学儿童重返校园，某社区组织“献爱心手拉手”捐款活动. 对社区部分捐款户数进行调查和分组统计后，将数据整理成如图所示的统计图（图中信息不完整）. 已知A、B两组捐款户数的比为1 : 5.
|
请结合以上信息解答下列问题.
(1)a= ，本次调查样本的容量是 ；
(2) 先求出C组的户数，再补全“捐款户数分组统计图1”；
(3) 若该社区有500户住户，请根据以上信息估计，全社区捐款不少于300元的户数是多少？
相关知识点
推荐套卷
粤公网安备 44130202000953号