如图，抛物线l1:y=－x2＋2bx＋c（b＞0）的顶点为A,与y轴交于点B;若抛物线l2与l1关于原点O成中心对称，其顶点为C , 与y轴交于点D;其中点A、B、C、D中的任意三点都不在同一条直线上
（1）顺次连接四点得四边形ABCD，则四边形ABCD形状是______________。
（2）请你探究：四边形ABCD能否成为正方形？若能，求出符合条件的b，c的值；若不能，请说明理由．
（3）继续探究：四边形ABCD是邻边之比为1:2的矩形时，求b，c的值。
相关试题
,其中x=-1,y=2.
在平面直角坐标系xoy中，边长为
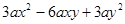
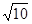的正方形ABCD的对角线AC、BD相交于点P，顶点A在x轴正半轴上运动，顶点B在y轴正半轴上运动（x轴的正半轴、y轴的正半轴都不包含原点O），顶点C、D都在第一象限．
⑴当∠BAO=45°时，求点P的坐标;
⑵求证：无论点A在x轴正半轴上、点B在y轴正半轴上怎样运动，点P都在∠AOB的平分线上；
⑶当B点坐标为（0,1）时，求CD的解析式。
某公司每月付给销售人员的工资有两种方案．
方案一：没有底薪，只拿销售提成；
方案二：底薪加销售提成
(注：销售提成是指从销售每件商品得到的销售额中提取一定数量的费用)．
设销售商品的数量
(件)，销售人员的月工资
(元)．如图所示，
为方案一的函数图象，
为方案二的函数图象．从图中信息解答如下问题：
⑴求的函数函数关系式；
⑵求点A的坐标，并说出A点的实际意义；
⑶请问方案二中每月付给销售人员的底薪是多少元？
⑷如果该公司销售人员小丽的月工资要不低于1800元，那么小丽选用哪种方案最好？至少要销售商品多少件？
相关知识点
推荐套卷
粤公网安备 44130202000953号