（本小题满分13分）已知椭圆
过点
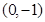，且离心率
．
（1）求椭圆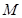
的方程；
（2）是否存在菱形
，同时满足下列三个条件：
①点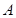
在直线
上；
②点
，
，
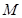在椭圆上；
③直线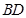
的斜率等于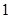
．
如果存在，求出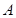点坐标；如果不存在，说明理由．
相关试题
是边长为4的正三角形，
底面
，点
是
的中点，点
在
上，且
．
平面
；
的体积．
中，已知
．
的值．
．
的不等式
；
的解集非空，求实数
的取值范围．
，曲线C与
有且仅有一个公共点．
的值；
，求
的最大值．
中，
是
的角平分线，
的外接圆交
于点
，
．
；
时，求
的长．推荐套卷
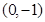（本小题满分13分）已知椭圆过点，且离心率．
（1）求椭圆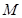的方程；
（2）是否存在菱形，同时满足下列三个条件：
①点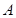在直线上；
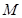②点，，在椭圆上；
③直线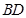的斜率等于．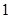
如果存在，求出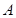点坐标；如果不存在，说明理由．
粤公网安备 44130202000953号