（本小题满分13分）已知动点P到定点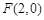
的距离和它到定直线
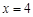的距离的比值为
．
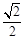（Ⅰ）求动点P的轨迹W的方程；
（Ⅱ）若过点F的直线与点P的轨迹W相交于M，N两点（M，N均在y轴右侧），点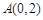
、
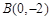，设A，B，M，N四点构成的四边形的面积为S，求S的取值范围．
相关试题
＞0;(2)9x2-6x+1≥0.
＞0 (a∈R).
≥
(x2-9)-3x.推荐套卷
（本小题满分13分）已知动点P到定点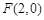的距离和它到定直线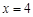的距离的比值为．
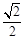（Ⅰ）求动点P的轨迹W的方程；
（Ⅱ）若过点F的直线与点P的轨迹W相交于M，N两点（M，N均在y轴右侧），点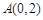、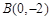，设A，B，M，N四点构成的四边形的面积为S，求S的取值范围．
粤公网安备 44130202000953号