(本小题14分)已知函数 在其定义域上满足:
在其定义域上满足: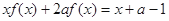 ,
,
(1)函数 的图象是否是中学对称图形?若是,请指出其对称中心(不证明)
的图象是否是中学对称图形?若是,请指出其对称中心(不证明)
(2)当 时,求
时,求 的取值范围
的取值范围
(3)若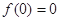 ,数列
,数列 满足
满足 ,那么若
,那么若 正整数N满足n>N时,对所有适合上述条件的数列
正整数N满足n>N时,对所有适合上述条件的数列 ,
,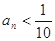 恒成立,求最小的N.
恒成立,求最小的N.
推荐套卷
(本小题14分)已知函数 在其定义域上满足:
在其定义域上满足: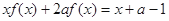 ,
,
(1)函数 的图象是否是中学对称图形?若是,请指出其对称中心(不证明)
的图象是否是中学对称图形?若是,请指出其对称中心(不证明)
(2)当 时,求
时,求 的取值范围
的取值范围
(3)若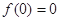 ,数列
,数列 满足
满足 ,那么若
,那么若 正整数N满足n>N时,对所有适合上述条件的数列
正整数N满足n>N时,对所有适合上述条件的数列 ,
,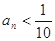 恒成立,求最小的N.
恒成立,求最小的N.