（本小题满分12分）某校进行教工趣味运动会，其中一项目是投篮比赛，规则是：每位教师投二分球四次，投中三个可以再投三分球一次，投中四个可以再投三分球三次，投中球数小于3则没有机会投三分球，所有参加的老师都可以获得一个小奖品，每投中一个三分球可以再获得一个小奖品。某位教师二分球的命中率是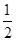
，三分球的命中率是
．
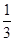（Ⅰ）求该教师恰好投中四个球的概率；
（Ⅱ）记该教师获得奖品数为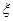
，求随机变量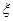的分布列和数学期望．
相关试题
=an(Sn-
).
，求{bn}的前n项和Tn.
+
+
+…+
.
,a1=2,求数列{an}的通项公式.
f(bn-1) (n∈N,n≥2),求证：
为等差数列，并求bn.推荐套卷
（本小题满分12分）某校进行教工趣味运动会，其中一项目是投篮比赛，规则是：每位教师投二分球四次，投中三个可以再投三分球一次，投中四个可以再投三分球三次，投中球数小于3则没有机会投三分球，所有参加的老师都可以获得一个小奖品，每投中一个三分球可以再获得一个小奖品。某位教师二分球的命中率是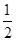，三分球的命中率是．
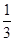（Ⅰ）求该教师恰好投中四个球的概率；
（Ⅱ）记该教师获得奖品数为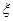，求随机变量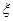的分布列和数学期望．
粤公网安备 44130202000953号