如图,平行四边形ABCD在平面直角坐标系中,点A的坐标为(-2,0),点B的坐标为(0,4),抛物线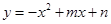 经过点A和C.
经过点A和C.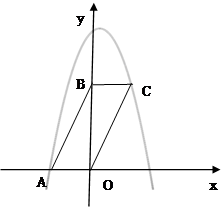
(1)求抛物线的解析式.
(2)该抛物线的对称轴将平行四边形ABCO分成两部分,对称轴左侧部分的图形面积记为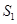 ,右侧部分图形的面积记为
,右侧部分图形的面积记为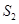 ,求
,求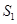 与
与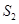 的比.
的比.
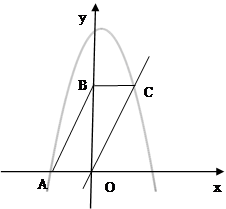
(3)在y轴上取一点D,坐标是(0,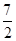 ),将直线OC沿x轴平移到
),将直线OC沿x轴平移到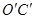 ,点D关于直线
,点D关于直线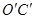 的对称点记为
的对称点记为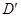 ,当点
,当点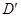 正好在抛物线上时,求出此时点
正好在抛物线上时,求出此时点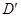 坐标并直接写出直线
坐标并直接写出直线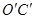 的函数解析式.
的函数解析式.
相关知识点
推荐套卷
 在数轴上的位置如图所示,化简
在数轴上的位置如图所示,化简 .
.
 ,求此函数的解析式。
,求此函数的解析式。 ,其中
,其中 .
. ,求
,求 的值
的值 为实数,且
为实数,且 ,求
,求 的值.
的值. ,求下列各式的值:
,求下列各式的值: (2)
(2)
 粤公网安备 44130202000953号
粤公网安备 44130202000953号