如图，二次函数y=ax2+bx+c的图象交x轴于A（﹣1，0），B（2，0），交y轴于C（0，﹣2），过A，C画直线．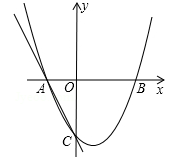
（1）求二次函数的解析式；
（2）点P在x轴正半轴上，且PA=PC，求OP的长；
（3）若M为线段OB上一个动点，过点M作MN平行于y轴交抛物线于点N，当点M运动到何处时，四边形ACNB的面积最大？求出此时点M的坐标及四边形ACNB面积的最大值．
相关试题
如图，二次函数y=ax2+bx+c的图象交x轴于A（﹣1，0），B（2，0），交y轴于C（0，﹣2），过A，C画直线．
（1）求二次函数的解析式；
（2）点P在x轴正半轴上，且PA=PC，求OP的长；
（3）若M为线段OB上一个动点，过点M作MN平行于y轴交抛物线于点N，当点M运动到何处时，四边形ACNB的面积最大？求出此时点M的坐标及四边形ACNB面积的最大值．
、
、
在数轴上的位置如图：
．
的值．
，其中：
， 
．
，﹣|﹣3|，
，﹣（﹣2）在数轴上表示出来，并用“＜”把他们连接起来．
粤公网安备 44130202000953号