给定有限单调递增数列 ,数列
,数列 至少有两项)且
至少有两项)且
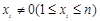 ,定义集合
,定义集合 .若对任意点
.若对任意点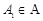 ,
,
存在点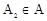 使得
使得
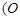 为坐标原点),则称数列
为坐标原点),则称数列 具有性质
具有性质 .
.
(1)给出下列四个命题,其中正确的是 .(填上所有正确命题的序号)
①数列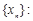 -2,2具有性质
-2,2具有性质 ;
;
②数列 :-2,-1,1,3具有性质
:-2,-1,1,3具有性质 ;
;
③若数列 具有性质
具有性质 ,则
,则 中一定存在两项
中一定存在两项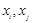 ,使得
,使得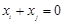 ;
;
④若数列 具有性质
具有性质 ,
,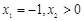 且
且 ,则
,则 .
.
(2)若数列 只有2014项且具有性质
只有2014项且具有性质 ,则
,则 的所有项和
的所有项和 .
.
相关知识点
推荐套卷
 、
、 是三次函数
是三次函数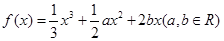 的两个极值点,且
的两个极值点,且 ,
, ,则
,则 的取值范围是
的取值范围是 .
.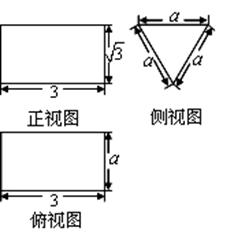
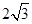 ,点D 在BC边上,∠ADC=60°,则
,点D 在BC边上,∠ADC=60°,则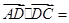 ______.
______.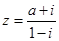 (
(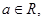
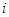 是虚数单位)是纯虚数,则
是虚数单位)是纯虚数,则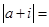
 其一半,图(3)用图(2)的方法在每一线段前端生成两条线段,长度为其一半,重复前面的作法至第n张图,设第n个图形所有线段长之和为an,第n个图形,最短的线段长之和为bn,设
其一半,图(3)用图(2)的方法在每一线段前端生成两条线段,长度为其一半,重复前面的作法至第n张图,设第n个图形所有线段长之和为an,第n个图形,最短的线段长之和为bn,设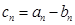 ,则cn=
,则cn=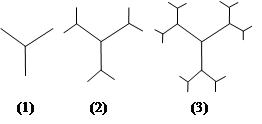
 粤公网安备 44130202000953号
粤公网安备 44130202000953号