如图,直线 和x轴、y轴的交点分别为B、C,点A的坐标是(﹣2,0).
和x轴、y轴的交点分别为B、C,点A的坐标是(﹣2,0).
(1)试说明△ABC是等腰三角形;
(2)动点M从A出发沿x轴向点B运动,同时动点N从点B出发沿线段BC向点C运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M运动t秒时,△MON的面积为S.
①求S与t的函数关系式;
②设点M在线段OB上运动时,是否存在S=4的情形?若存在,求出对应的t值;若不存在请说明理由;
③在运动过程中,当△MON为直角三角形时,求t的值.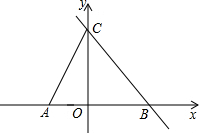
如图,直线 和x轴、y轴的交点分别为B、C,点A的坐标是(﹣2,0).
和x轴、y轴的交点分别为B、C,点A的坐标是(﹣2,0).
(1)试说明△ABC是等腰三角形;
(2)动点M从A出发沿x轴向点B运动,同时动点N从点B出发沿线段BC向点C运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M运动t秒时,△MON的面积为S.
①求S与t的函数关系式;
②设点M在线段OB上运动时,是否存在S=4的情形?若存在,求出对应的t值;若不存在请说明理由;
③在运动过程中,当△MON为直角三角形时,求t的值.