若四面体
的三组对棱分别相等，即
，
，
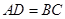，则 .
①四面体每组对棱相互垂直
②四面体每个面的面积相等
③从四面体每个顶点出发的三条棱两两夹角之和大于
而小于
④连接四面体每组对棱中点的线段互相垂直平分
⑤从四面体每个顶点出发的三条棱的长可作为一个三角形的三边长
）（1+
）的导数为．
+2，f（1）+f′（1）=．
t2，t=3s时，此木块在水平方向上的瞬时速度为．推荐套卷
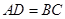若四面体的三组对棱分别相等，即，，，则 .
①四面体每组对棱相互垂直
②四面体每个面的面积相等
③从四面体每个顶点出发的三条棱两两夹角之和大于而小于
④连接四面体每组对棱中点的线段互相垂直平分
⑤从四面体每个顶点出发的三条棱的长可作为一个三角形的三边长
粤公网安备 44130202000953号