将一圆的六个等分点分成两组相间的三点﹐它们所构成的两个正三角形扣除内部六条线段后可以形成一正六角星﹐如图所示的正六角星是以原点
为中心﹐其中
,分别为原点到两个顶点的向量﹒若将原点到正六角星12个顶点的向量﹐都写成为
的形式﹐则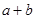
的最大值为（ ）。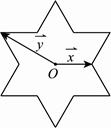
| A．2 | B．3 | C．4 | D．5 |
，则输出的
等于（）
满足约束条件
，则
的最小值为（）
满足
，
，则
满足
，则
（）
推荐套卷
将一圆的六个等分点分成两组相间的三点﹐它们所构成的两个正三角形扣除内部六条线段后可以形成一正六角星﹐如图所示的正六角星是以原点为中心﹐其中,分别为原点到两个顶点的向量﹒若将原点到正六角星12个顶点的向量﹐都写成为的形式﹐则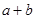的最大值为（ ）。
| A．2 | B．3 | C．4 | D．5 |
粤公网安备 44130202000953号