如图，矩形ABCD的四个顶点的坐标分别为A（0,—1），B（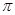
,—1），C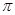（,1），D（0,1），正弦曲线
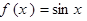和余弦曲线
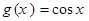在矩形ABCD内交于点F，向矩形ABCD区域内随机投掷一点，则该点落在阴影区域内的概率是（ ）．
A． |
B． |
C． |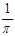
D． |
相关试题
，
，向量
与
垂直，则实数
的值为（）
中，
，
，则
（）
的值等于（）
，
，满足条件的△ABC （）相关知识点
推荐套卷
如图，矩形ABCD的四个顶点的坐标分别为A（0,—1），B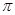（,—1），C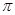（,1），D（0,1），正弦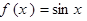曲线和余弦曲线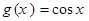在矩形ABCD内交于点F，向矩形ABCD区域内随机投掷一点，则该点落在阴影区域内的概率是（ ）．
| A． |
B． |
C． |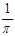
D． |
粤公网安备 44130202000953号