如图所示，在平面直角坐标系中，一个方格的边长为1个单位长度，△MNQ是△ABC经过某种变化后得到的图形，请分别写出对应点：点A与点M，点B与点N，点C与点Q的坐标，并观察它们的坐标之间的关系．如果△ABC中任何一点P的坐标为（x，y），那么其对应点R的坐标是什么？猜想线段AC与线段MQ的关系．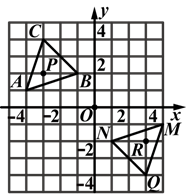
如图所示，在平面直角坐标系中，一个方格的边长为1个单位长度，△MNQ是△ABC经过某种变化后得到的图形，请分别写出对应点：点A与点M，点B与点N，点C与点Q的坐标，并观察它们的坐标之间的关系．如果△ABC中任何一点P的坐标为（x，y），那么其对应点R的坐标是什么？猜想线段AC与线段MQ的关系．
）×（-30）
．
；
．
粤公网安备 44130202000953号