(本小题满分12分)为了响应学校“学科文化节”活动,数学组举办了一场数学知识竞赛,共分为甲、乙两组.其中甲组得满分的有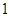 个女生和
个女生和 个男生,乙组得满分的有
个男生,乙组得满分的有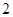 个女生和
个女生和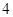 个男生.现从得满分的学生中,每组各任选
个男生.现从得满分的学生中,每组各任选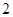 个学生,作为数学组的活动代言人.
个学生,作为数学组的活动代言人.
(1)求选出的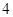 个学生中恰有
个学生中恰有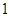 个女生的概率;
个女生的概率;
(2)设 为选出的
为选出的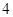 个学生中女生的人数,求
个学生中女生的人数,求 的分布列和数学期望.
的分布列和数学期望.
推荐套卷
(本小题满分12分)为了响应学校“学科文化节”活动,数学组举办了一场数学知识竞赛,共分为甲、乙两组.其中甲组得满分的有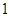 个女生和
个女生和 个男生,乙组得满分的有
个男生,乙组得满分的有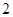 个女生和
个女生和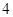 个男生.现从得满分的学生中,每组各任选
个男生.现从得满分的学生中,每组各任选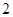 个学生,作为数学组的活动代言人.
个学生,作为数学组的活动代言人.
(1)求选出的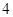 个学生中恰有
个学生中恰有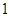 个女生的概率;
个女生的概率;
(2)设 为选出的
为选出的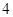 个学生中女生的人数,求
个学生中女生的人数,求 的分布列和数学期望.
的分布列和数学期望.