下图展示了一个由区间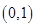 到实数集
到实数集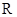 的映射过程:区间
的映射过程:区间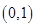 中的实数
中的实数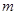 对应数轴上的点
对应数轴上的点 (点
(点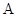 对应实数
对应实数 ,点
,点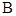 对应实数
对应实数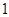 ),如图①;将线段
),如图①;将线段 围成一个圆,使两端点
围成一个圆,使两端点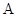 、
、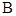 恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在
恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在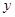 轴上,点
轴上,点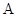 的坐标为
的坐标为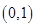 ,在图形变化过程中,图①中线段
,在图形变化过程中,图①中线段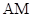 的长度对应于图③中的弧
的长度对应于图③中的弧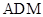 的长度,如图③,图③中直线
的长度,如图③,图③中直线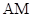 与
与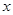 轴交于点
轴交于点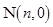 ,则
,则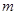 的象就是
的象就是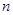 ,记作
,记作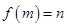 .给出下列命题:①
.给出下列命题:①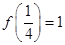 ;②
;②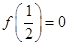 ;③
;③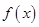 是奇函数;④
是奇函数;④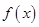 在定义域上单调递增,则所有真命题的序号是( )
在定义域上单调递增,则所有真命题的序号是( )
| A.①② | B.②③ | C.①④ | D.②④ |
相关知识点
推荐套卷
 ,
,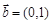 ,若
,若 与
与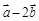 平行,则
平行,则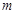 等于()
等于()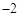
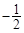

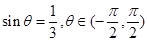 ,则
,则 的值是()
的值是()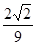
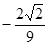
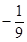

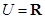 ,集合
,集合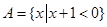 ,
, ,那么集合
,那么集合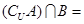 ( )
( )
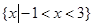
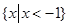
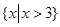
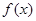 是定义在R上的奇函数,
是定义在R上的奇函数,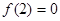 ,当
,当 成立,则不等式
成立,则不等式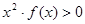 的解集是
的解集是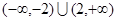
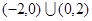
 粤公网安备 44130202000953号
粤公网安备 44130202000953号